Terence Z. Liu

ML / Data / Platform
Ph.D.


The Wonders of RocksDB in Rust (Part II - Set Operations)

Feb 11, 2026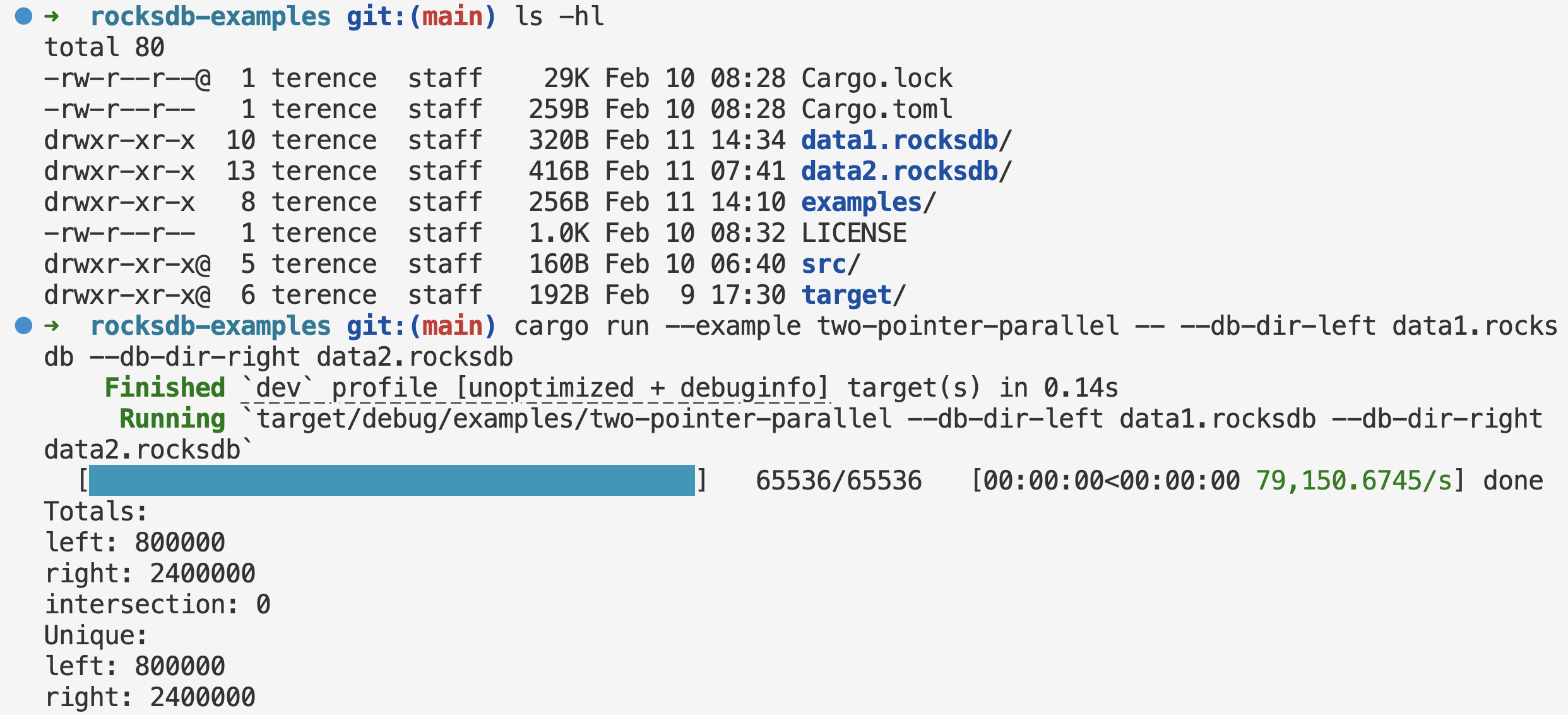

img

You can check out the code here.

How does one get the intersection of two sorted lists in memory?

One could simply convert each list into a hash set to get the intersection. The time complexity is O(n + m) for the conversion, and O(min(n, m)) for the intersection, with n and m being the lengths of the two lists. The hash set lookup is constant. The space complexity is O(n + m) for the conversion.

def get_intersection(list1: list[int], list2: list[int]) -> set:
    set1 = set(list1)
    set2 = set(list2)
    return set1 & set2

You could get away with converting only one list, then iterate through the other list to check if the element is in the set. The time complexity is still O(n + m) and the space complexity is O(n). This is how DuckDB and Polars do it. For equi-joins (match by equality), both use the same idea: hash join — build a hash table on one side (usually the smaller), then probe with the other. So it’s the same O(n + m) time complexity and O(n) space complexity, just at columnar scale with SIMD and careful memory layout. When the build side doesn’t fit in memory, DuckDB switches to a partitioned out-of-core hash join (spill to disk, then merge). Polars’ streaming engine processes in batches but does not spill join state to disk — joins can still be memory-heavy or fall back to the in-memory engine, so very large joins may OOM.

A Tale of Two Pointers

What if you have way too much data, and don’t want the conversion overhead and disk spilling? Consider two tables with several TBs each. Turns out you can do a lot with the sortedness property. One could iterate through the shorter list and check if the element is in the longer list by binary search. The time complexity is O(n log m), n being the length of the shorter list. This can be worse than the hash set approach if the two list lengths are similar. A better approach in that case is to use the two-pointer technique to get the intersection in one pass. You can in fact get all the set logic counts in one pass. The time complexity is again O(n + m). These two approaches have no additional space complexity.

To keep it simple, let’s still use two lists in memory for the example.

count_left, count_right, count_intersection = 0, 0, 0
i, j = 0, 0

while i < len(list1) and j < len(list2):
    if list1[i] == list2[j]:
        count_left += 1
        count_right += 1
        count_intersection += 1
        i += 1
        j += 1
    elif list1[i] < list2[j]:
        count_left += 1
        i += 1
    else:
        count_right += 1
        j += 1

# drain remaining elements
while i < len(list1):
    count_left += 1
    i += 1

while j < len(list2):
    count_right += 1
    j += 1

Two RocksDBs, One Pass

Now let’s say you have two RocksDBs with similar data. The keys are hex strings emulating hashes. You want to draw the Venn diagram of the two sets of keys. The two-pointer approach is perfect for this, because the sorted string table (SST) files are already sorted. So you can do something similar (full code):

let db_left = open_rocksdb_for_read_only(&args.db_dir_left, true)?;
let db_right = open_rocksdb_for_read_only(&args.db_dir_right, true)?;

let mut db_iter_left = db_left.full_iterator(IteratorMode::Start);
let mut db_iter_right = db_right.full_iterator(IteratorMode::Start);

let mut count_left = 0;
let mut count_right = 0;
let mut count_intersection = 0;
let mut item_left = db_iter_left.next();
let mut item_right = db_iter_right.next();

// Don't use take() — we must keep the item we don't advance so it's compared again next iteration.
while let (Some(Ok((blob_left, _))), Some(Ok((blob_right, _)))) =
    (item_left.as_ref(), item_right.as_ref())
{
    if blob_left == blob_right {
        count_left += 1;
        count_right += 1;
        count_intersection += 1;
        item_left = db_iter_left.next();
        item_right = db_iter_right.next();
    } else if blob_left < blob_right {
        count_left += 1;
        item_left = db_iter_left.next();
    } else {
        count_right += 1;
        item_right = db_iter_right.next();
    }
}

while item_left.is_some() {
    count_left += 1;
    item_left = db_iter_left.next();
}

while item_right.is_some() {
    count_right += 1;
    item_right = db_iter_right.next();
}

Run in Parallel

We can adapt the two-pointer technique to run in parallel with the parallel scan pattern in Part I (full code):

let db_left = open_rocksdb_for_read_only(&args.db_dir_left, true)?;
let db_right = open_rocksdb_for_read_only(&args.db_dir_right, true)?;

let prefixes = generate_consecutive_hex_strings(4);
let pb = make_progress_bar(Some(prefixes.len() as u64));

let counts = prefixes
    .into_par_iter()
    .map(|prefix_str| {
        let prefix = prefix_str.as_bytes();

        let mut db_iter_left =
            db_left.full_iterator(IteratorMode::From(prefix, Direction::Forward));
        let mut db_iter_right =
            db_right.full_iterator(IteratorMode::From(prefix, Direction::Forward));

        // two pointers
        let mut count_left = 0;
        let mut count_right = 0;
        let mut count_intersection = 0;
        let mut item_left = db_iter_left.next();
        let mut item_right = db_iter_right.next();

        // Don't use take() — keep the item we don't advance for the next comparison.
        while let (Some(Ok((blob_left, _))), Some(Ok((blob_right, _)))) =
            (item_left.as_ref(), item_right.as_ref())
        {
            if &blob_left[..prefix.len()] != prefix || &blob_right[..prefix.len()] != prefix {
                break;
            }

            if blob_left == blob_right {
                count_left += 1;
                count_right += 1;
                count_intersection += 1;
                item_left = db_iter_left.next();
                item_right = db_iter_right.next();
            } else if blob_left < blob_right {
                count_left += 1;
                item_left = db_iter_left.next();
            } else {
                count_right += 1;
                item_right = db_iter_right.next();
            }
        }

        while let Some(Ok((blob_left, _))) = item_left.as_ref() {
            if &blob_left[..prefix.len()] != prefix {
                break;
            }
            count_left += 1;
            item_left = db_iter_left.next();
        }

        while let Some(Ok((blob_right, _))) = item_right.as_ref() {
            if &blob_right[..prefix.len()] != prefix {
                break;
            }
            count_right += 1;
            item_right = db_iter_right.next();
        }

        pb.inc(1);
        Counts {
            count_left,
            count_right,
            count_intersection,
        }
    })
    .reduce(
        || Counts {
            count_left: 0,
            count_right: 0,
            count_intersection: 0,
        },
        |accs, counts| Counts {
            count_left: accs.count_left + counts.count_left,
            count_right: accs.count_right + counts.count_right,
            count_intersection: accs.count_intersection + counts.count_intersection,
        },
    );

This is a very powerful pattern that can be used to solve a lot of problems. It can be used to get the intersection, union, difference, and symmetric difference of two sets of data, and apply arbitrary business logic to those parts of data.

Related Posts